Original Gibbs Phase rule :
Firstly, it is important to know about original Gibbs Phase Rule usually taught in all colleges and university, to build base for knowing their drawbacks and need of arising for modification to be made in this formula. Let's go !!
Simply, this rule stated that as - " Degree of freedom (F) is equal to number of intensive variable that can be changed independent without disturbing number of phases in equilibrium."
Equilibrium calculation involve intensive variables, which are independent of quantity and extensive variables, which depend on quantity.
When a certain number of variables (independent variables) are specified, then all other variables (dependent variables) are fixed. Then, number of independent variables is called variances or degree of freedom (F).
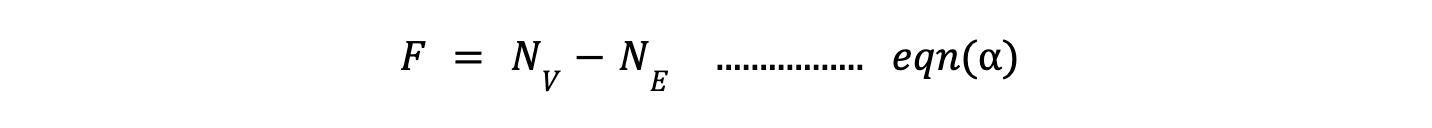
where:
- F = Degrees of freedom (number of independent variables needed to define the system).
- Nv = Number of variables in the system.
- Ne = Number of independent equations (constraints) imposed on the system, reducing degree of freedom effectively.
For defining Nv, let's say a system having C (number of component) existing in phases P (number of phases), each phase has C as number of independent mole fraction :
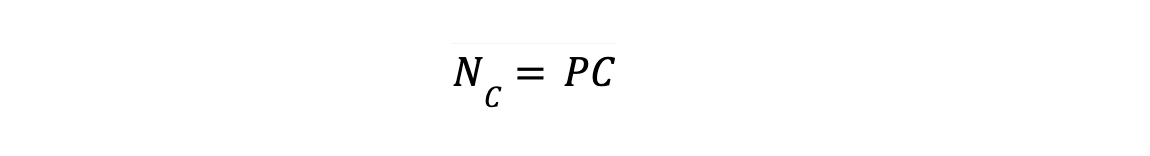
Besides of composition variables, we will also consider temperature and pressure as external variables because these are the same for all phases in equilibrium. So,
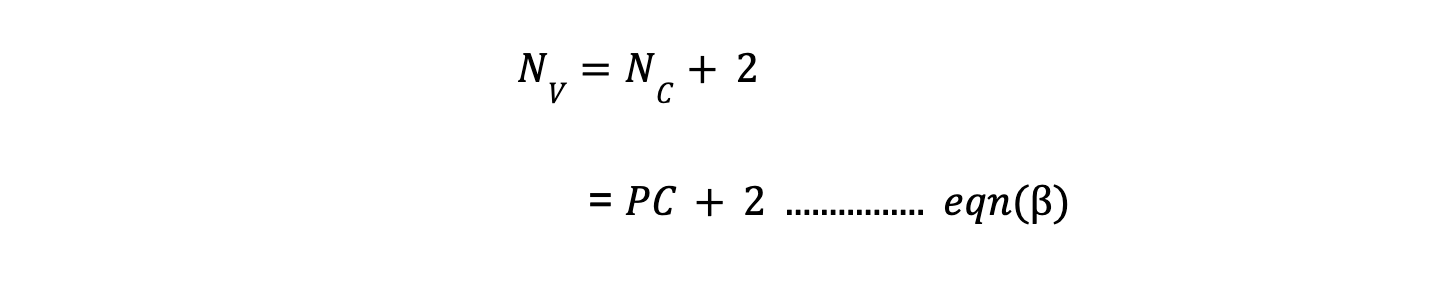
Now moving to Ne, as number of equation defining constraint being imposed on system. Majorly, we will consider two constraint :
- Mole fraction constraints: In each phase, mole fractions sum to 1.
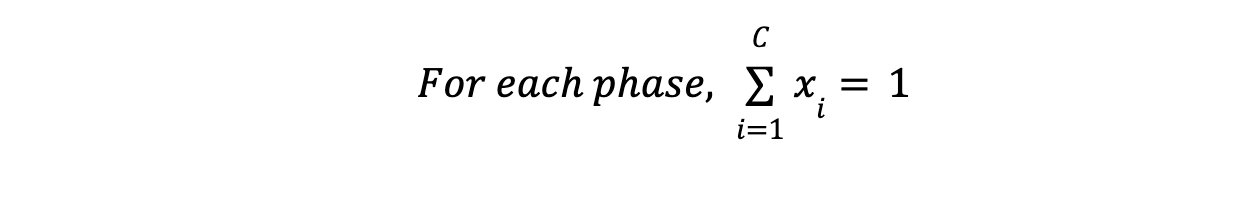
Similarly, we will define mole fraction constraint for rest of all other P, number of phases.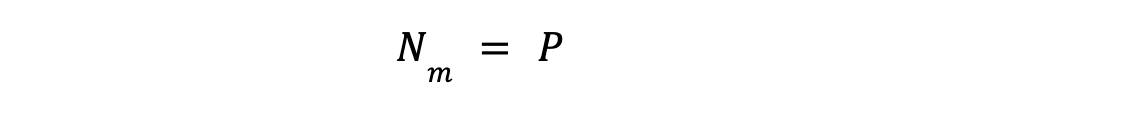
- Chemical potential equality: For each component i, its chemical potential (μi) must be equal in all P phases.
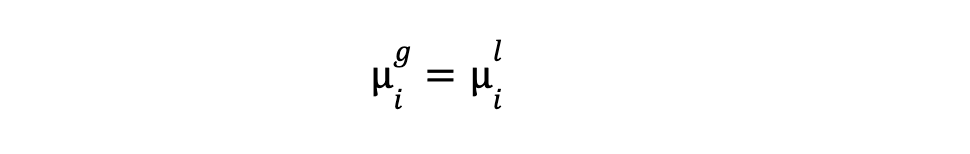
For C, components :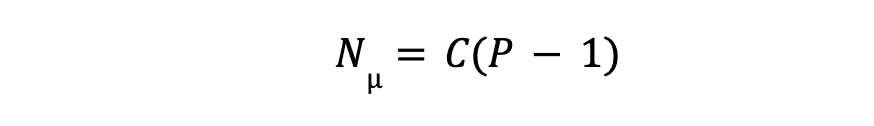
So, total number of equation (Ne) based on above two defined constraint, will be :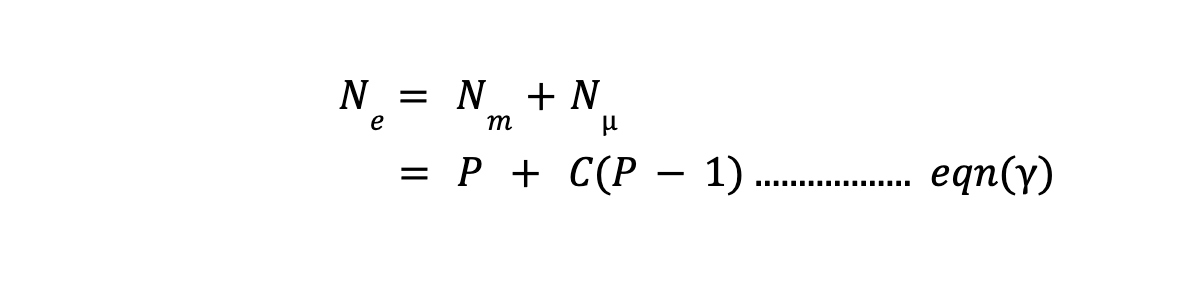
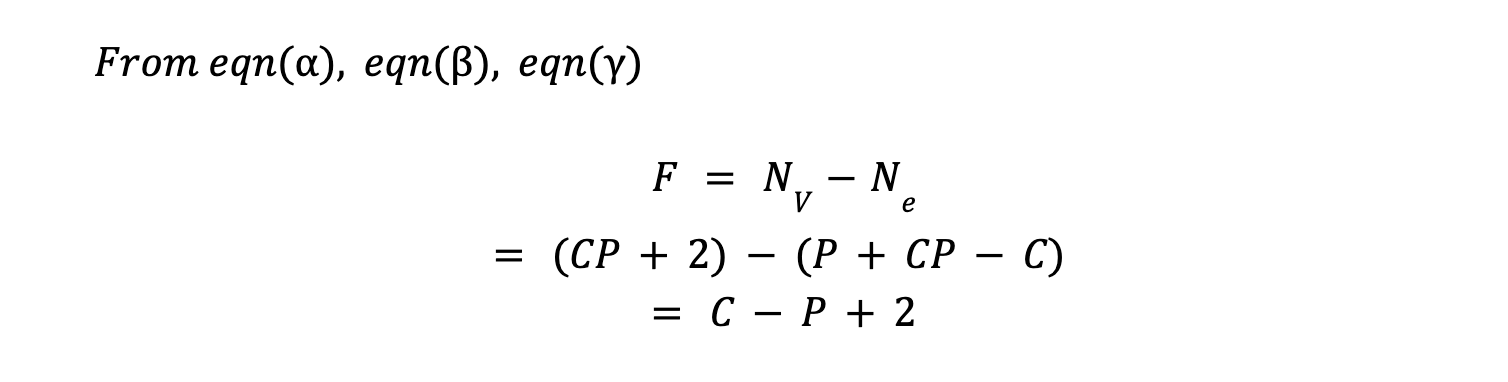
If R (number of independent reaction) happening in a system, then there will further addition of R in equation of constraint (Ne), reducing degree of freedom effectively by R.
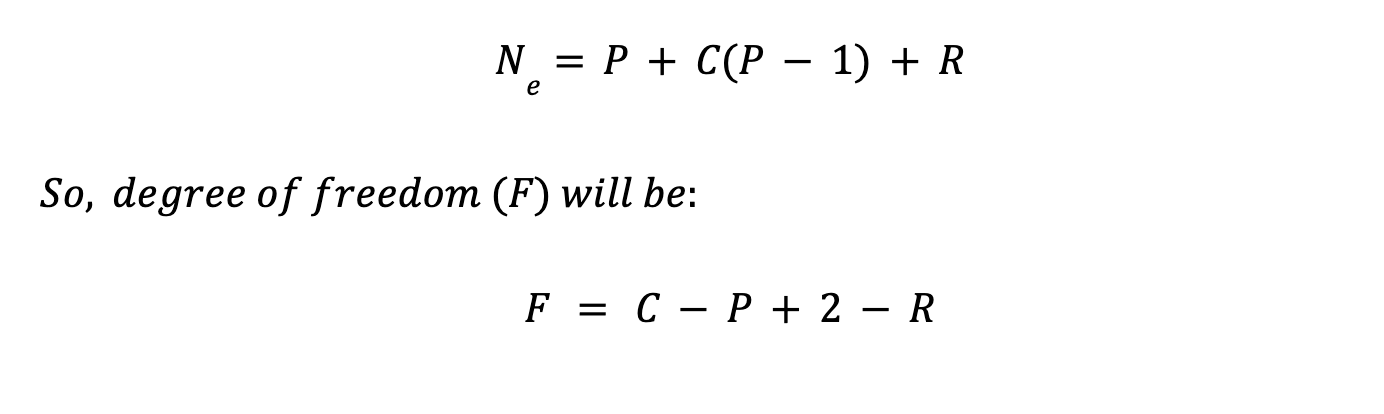
Methods and Finding :
The method includes analysing stoichiometric matrices for reaction dependencies and assessing non-ideal effects through activity and fugacity corrections. Data collection involves theoretical analysis and empirical validation through case studies in chemical engineering.
The findings demonstrate the effectiveness of the modified Gibbs Phase Rule in addressing limitations of the original rule. The study identifies key improvements in phase-specific classifications, reaction dependencies, and non-ideal effects, offering a effective framework for practical applications. The findings fill gaps in current understanding and provide solutions to previous challenges, enhancing the rule's applicability in complex systems.
Proposed and modified Gibbs phase rule, after doing various case-studies and validation with considering assumption and drawback :
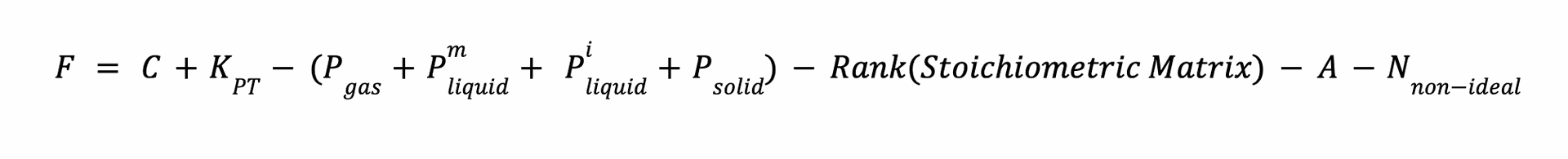

a. Enhanced Phase-Specific Classification : first key innovation
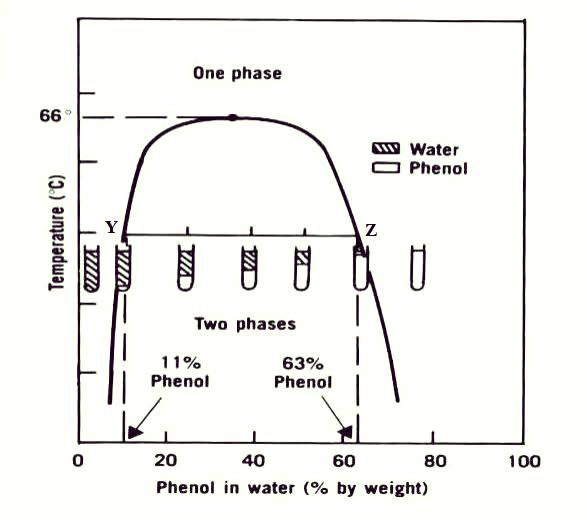
Initial studies applied the Gibbs Phase Rule uniformly across phases, leading to inaccuracies, especially in azeotropic and non-miscible systems. Later research introduced phase-specific classifications, distinguishing between gases, miscible, and non-miscible liquids, which improved accuracy, addressing previous inaccuracies in an azeotropic systems.
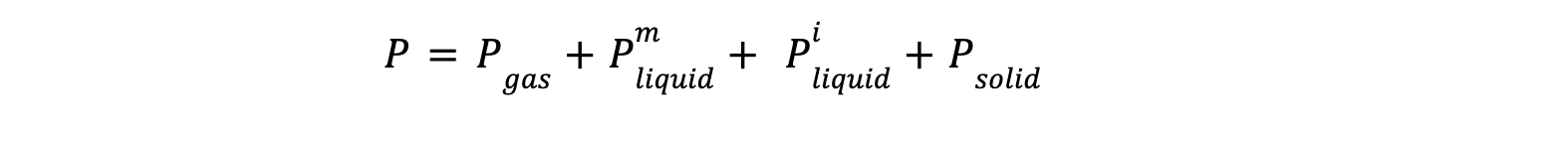


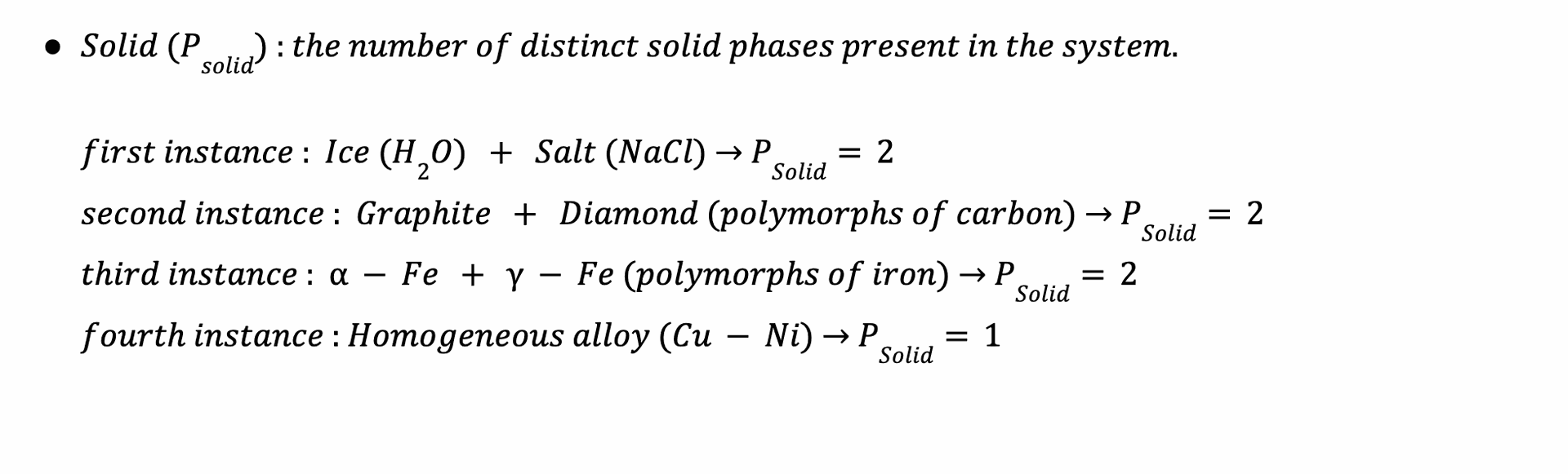
b. Azeotropic Constraint : second key innovation
'A' quantifies fixed composition constraints imposed by azeotropes in multi-component systems,:
- Binary Azeotropes: A = 1 (e.g., ethanol-water at 95.6% ethanol).
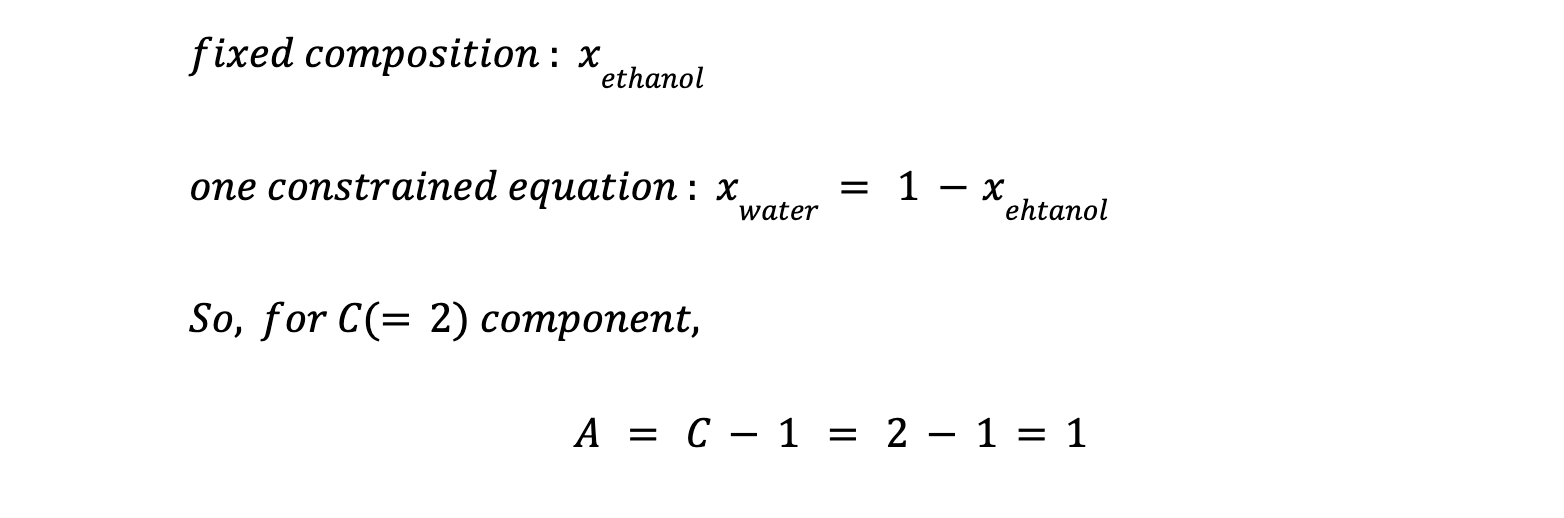
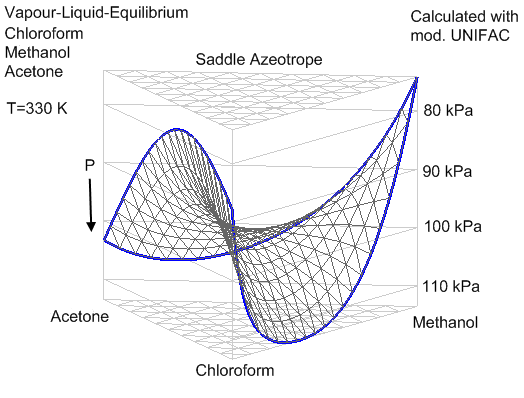
- Ternary Azeotropes: A = 2 (e.g., acetone-chloroform-methanol).

- General Rule: For C-component azeotropes, A = C − 1.
At the azeotropic point, liquid and vapor phases share identical compositions, eliminating one variable. The term A corrects the original Gibbs Rule’s failure to account for fixed compositions at azeotropes.
c. Improved Reaction Dependencies : third key innovation
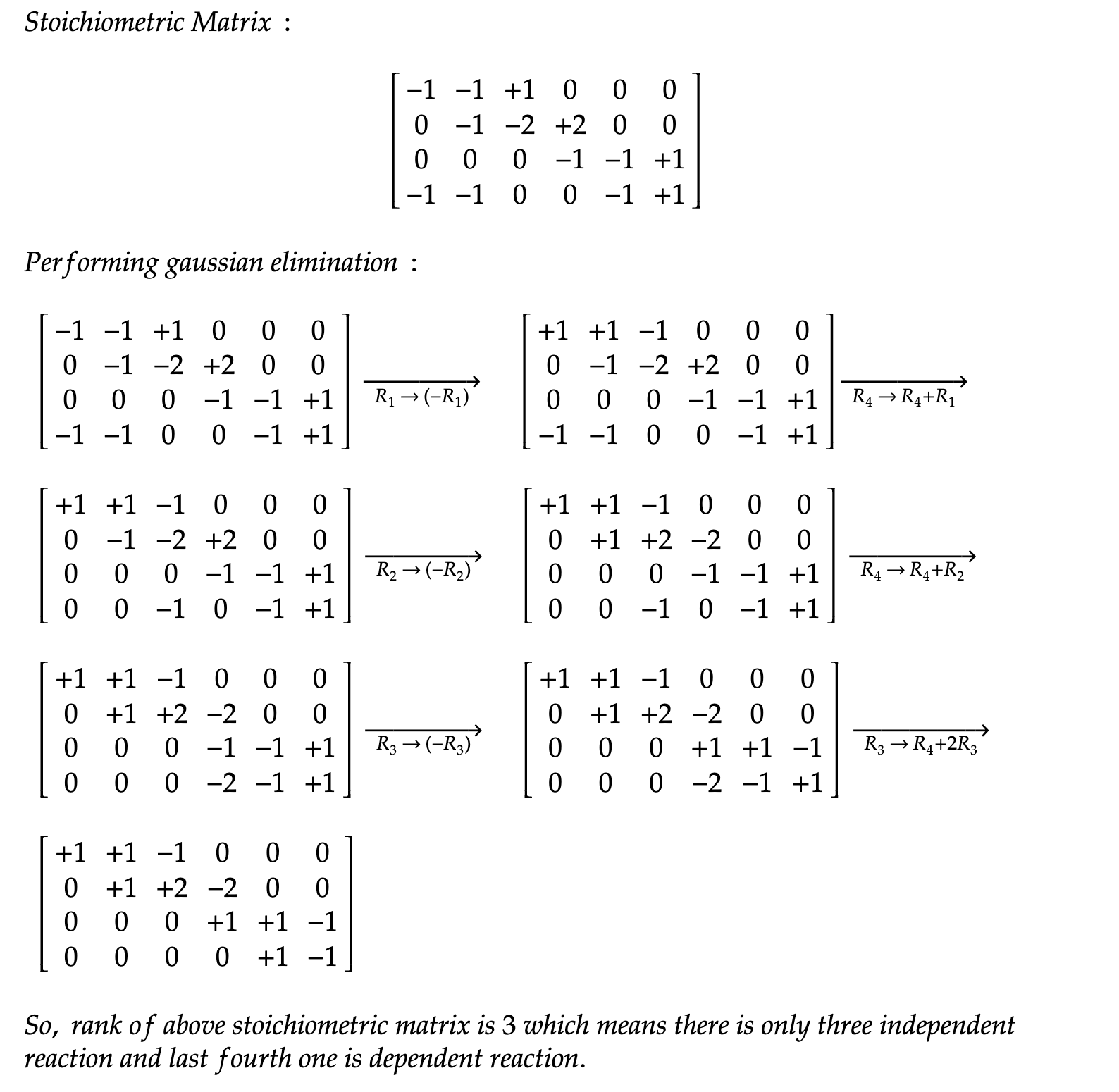
Considering reaction dependencies through stoichiometric matrix rank reduces overcounting and improves prediction. The analysis of methane reforming and ammonia synthesis showcases the benefits of this approach, offering solutions to previous limitations in handling reaction complexities.


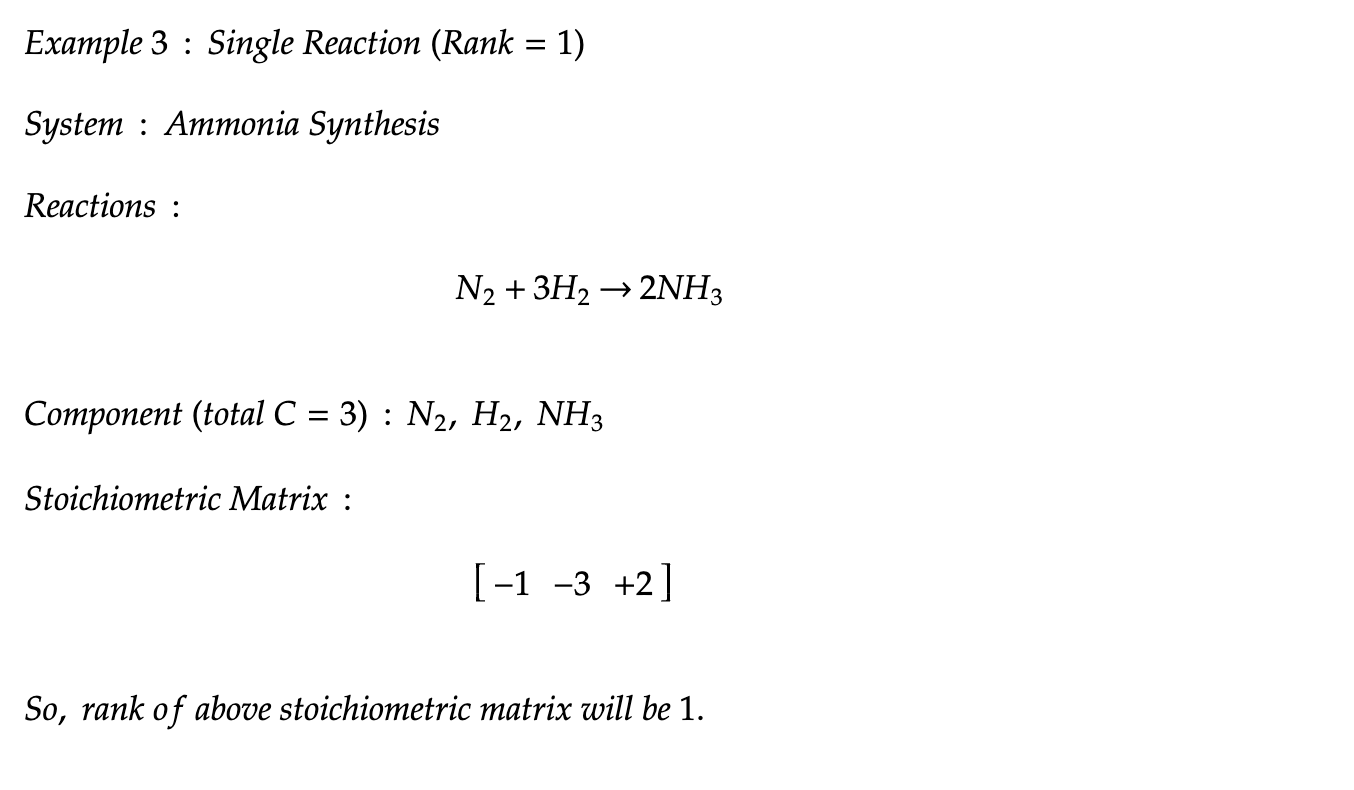

Addressing Non-Ideal Effects : Activity and Fugacity correction
Most systems exhibit non-ideal behavior mainly due to :
- Molecular Interactions: Hydrogen bonding, van der Waals forces, etc.
- Phase Behavior: Azeotropes, immiscibility, and complex equilibria.
- Real Gas Effects: Deviations from the ideal gas law at high pressures or low temperatures.
These deviations are modeled using (for different phases):
- Liquid Phases:
- Activity Coefficients (γi): Correct for deviations in liquid mixtures (e.g., ethanol-water azeotrope).
- Example: Margules, Van Laar, or NRTL equations model these deviations.
- Gas Phases:
- Fugacity Coefficients (ϕi): Adjust for real gas behavior (e.g., high-pressure CO₂).
- Example: Peng-Robinson or Redlich-Kwong equations of state.
Each non-ideal phase subtracts 1 degree of freedom due to additional constraints (e.g., composition corrections).

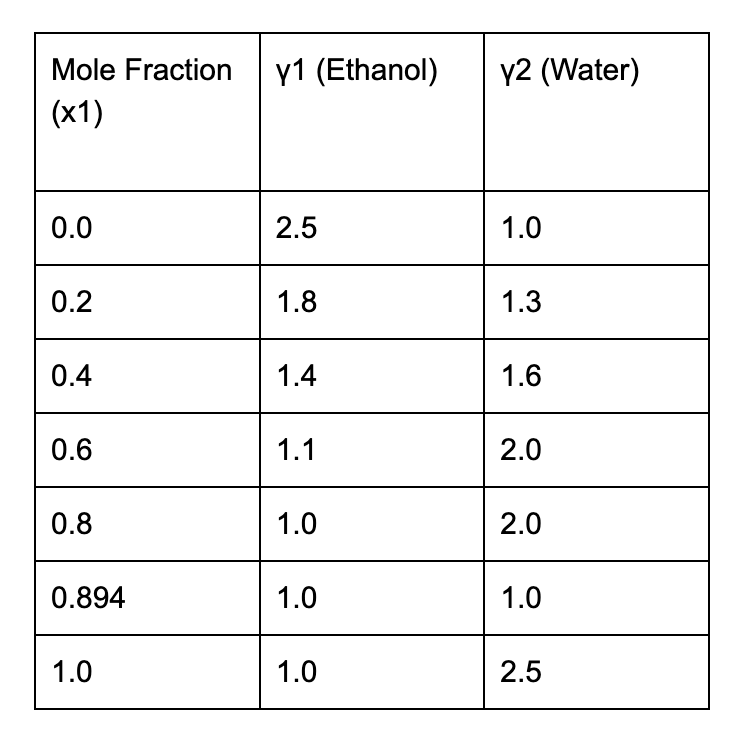
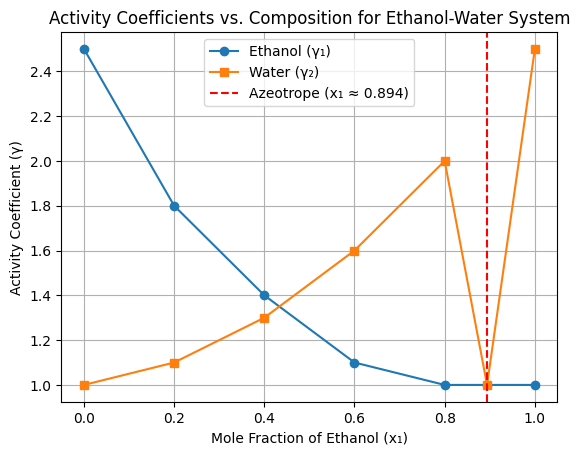
- At x1 = 0.0 (Pure Water):
- Ethanol is infinitely dilute, so γ1 is high (2.5), ethanol molecules experience strong interactions with water, leading to high γ1.
- Water is pure, so γ2 = 1.0
- At x1 = 0.894 (Azeotropic Composition):
- Both ethanol and water behave ideally (γ1 = γ2 = 1.0)
- This is the point where liquid and vapor compositions are equal.
- At x1 = 1.0 (Pure Ethanol):
- Water is infinitely dilute, so γ2 is high (2.5), water molecules experience strong interactions with ethanol, leading to high γ2.
- Ethanol is pure, so γ1 = 1.0


Case Studies with Validation :
Case Study-1 : High-pressure CO2 (fugacity correction)



Case Study-2: Ammonia Synthesis (single reaction system)


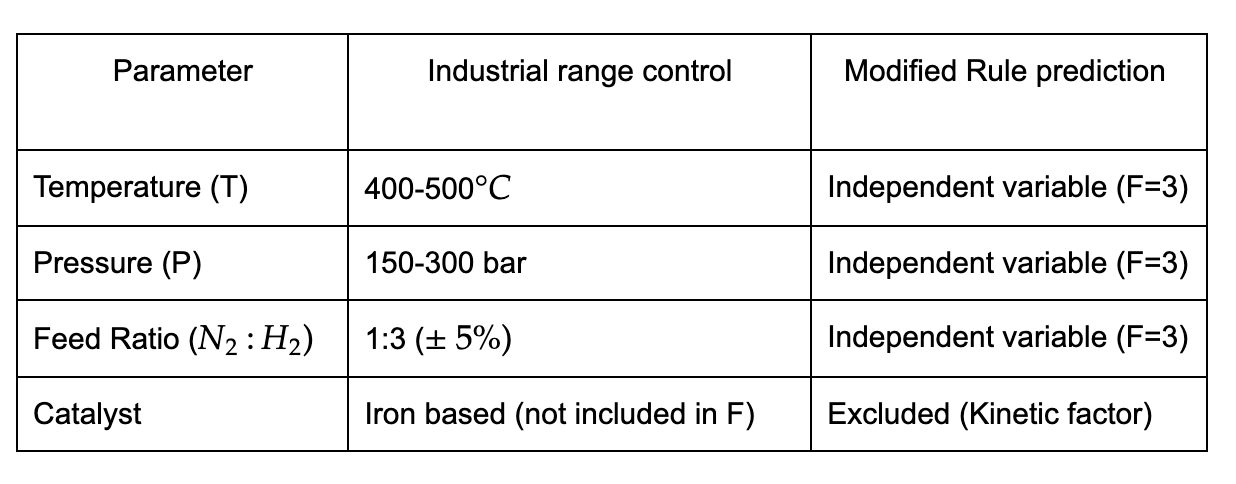
Case Study-3 : Catalytic reforming (multi-reaction system)


Conclusion
Although the journey of transforming the Gibbs Phase Rule into a more effective and practical framework has been challenging, it has also been worthy and rewarding. Through literature review, self-assumptions, and validation against industrial practices, I have attempted to bridge the gap between theoretical thermodynamics and real-world engineering.
We have seen how the modified Gibbs Phase Rule, with its incorporation of phase-specific terms, reaction dependencies, and non-ideal effects, proves invaluable for analyzing complex systems like ammonia synthesis, catalytic reforming, and high-pressure CO₂ processes—situations where the old rule falls short.
However, as the wise say, "Nothing is perfect." Theoretical predictions sometimes exceed practical control, as seen in the case of catalytic reforming due to fixed feed compositions, recycling constraints, and catalyst behavior. Despite these discrepancies, studying this rule remains crucial for developing a stronger foundation to understand and optimize chemical processes.
While the modified rule is thermodynamically sound, practical engineering often requires simplifying assumptions.
As we conclude, let this work inspire future researchers to embrace the challenges of independent inquiry, to question established norms, and to validate their ideas with the rigor of industrial relevance. In the end, it is not just about formulas or degrees of freedom—it is about accepting challenges and cherishing the joy of discovery and the impact of applied science.
