2.1 Various Forms of Energy and Total Energy
Energy can exist in numerous forms such as thermal, mechanical, kinetic, potential, electric, magnetic, chemical, and nuclear, and their sum constitutes the total energy E of a system.
Thermodynamics provides no information about the absolute value of the total energy. It deals only with changing the total energy used. The change in the total energy of a system is independent of the reference point selected.
2.1.1 Macroscopic and microscopic forms of energy
The macroscopic forms of energy are those a system possesses as a whole with respect to some outside reference frame, such as kinetic and potential energies.
The macroscopic energy of a system is related to motion and the influence of some external effects such as gravity, magnetism, electricity, and surface tension.
Kinetic Energy (K.E.) and Potential Energy (Macroscopic)
The energy that a system possesses as a result of its motion relative to some reference frame is called kinetic energy (KE).
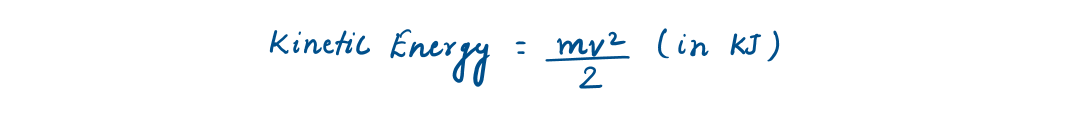
The kinetic energy of a rotating solid body is given by :
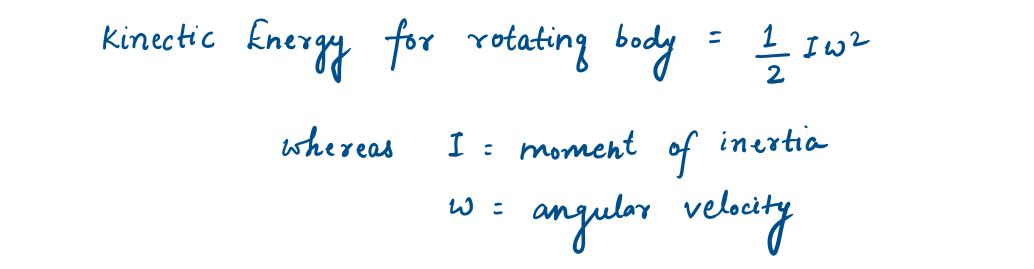
The energy that a system possesses as a result of its elevation in a gravitational field is called potential energy (PE).
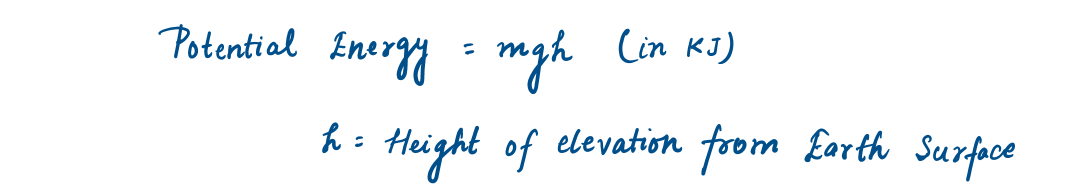
Internal Energy (Microscopic form of Energy)
The microscopic forms of energy are those related to the molecular structure of a system and the degree of molecular activity, and they are independent of outside reference frames.
The sum of all the microscopic forms of energy is called the internal energy of a system and is denoted by U.
2.1.2 Total Energy
In the absence of other small effects, the total energy of a system consists of the kinetic, potential, and internal energy and is expressed as
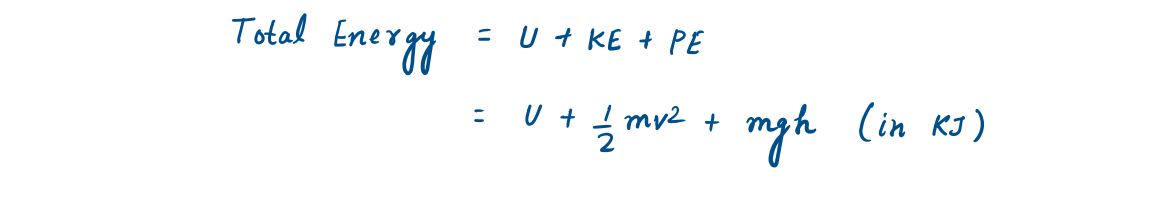
Most closed systems remain stationary during a process and thus experience no change in their kinetic and potential energies. Closed systems whose velocity and elevation of the center of gravity remain constant during a process are frequently referred to as stationary systems.
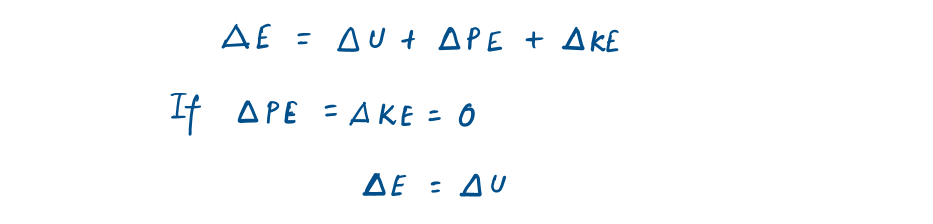
Hence, the change in the total energy (delta E) of a stationary system is identical to the change in its internal energy (delta U).
2.1.3 Mass flow rate and Energy flow rate
Generally, control volume (open system) involves fluid flow for a long time, hence it is more convenient to express energy flow associated with fluid stream in rate form. This is done by incorporating mass flow rate (M), which can be defined as:
'The amount of mass flowing through a cross-section per unit of time.'
It is related to the volume flow rate (V), which is the volume of a fluid flowing through a cross-section per unit time.
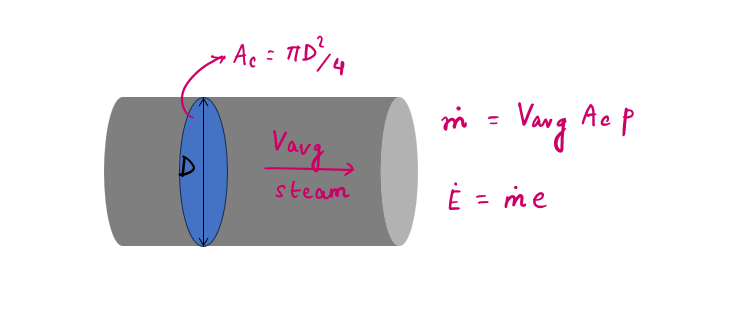
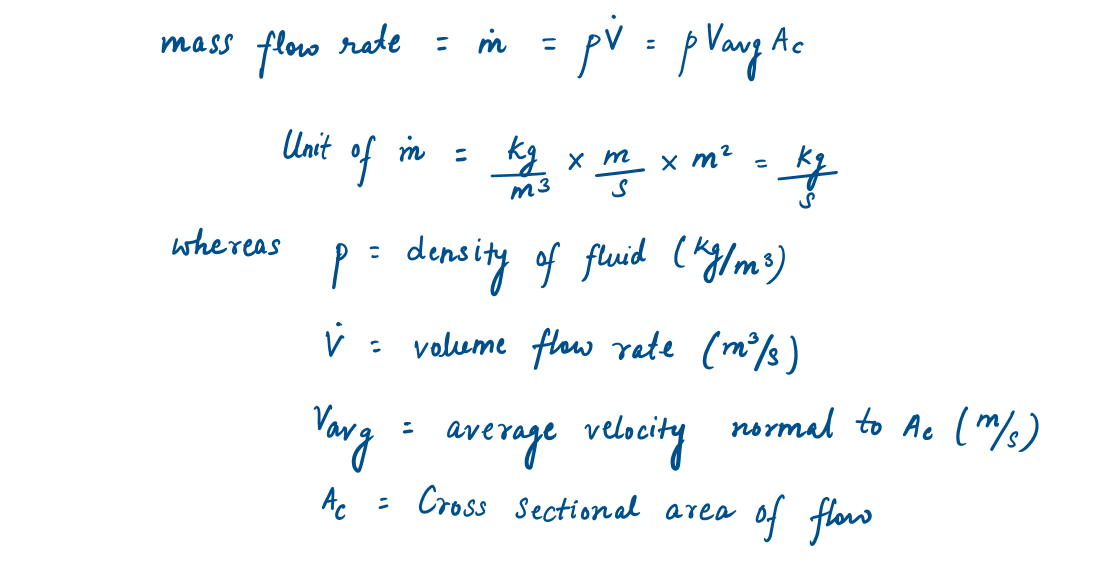
Similarly, the energy flow rate associated with a fluid flowing at a rate of M (mass flow rate), is given as:
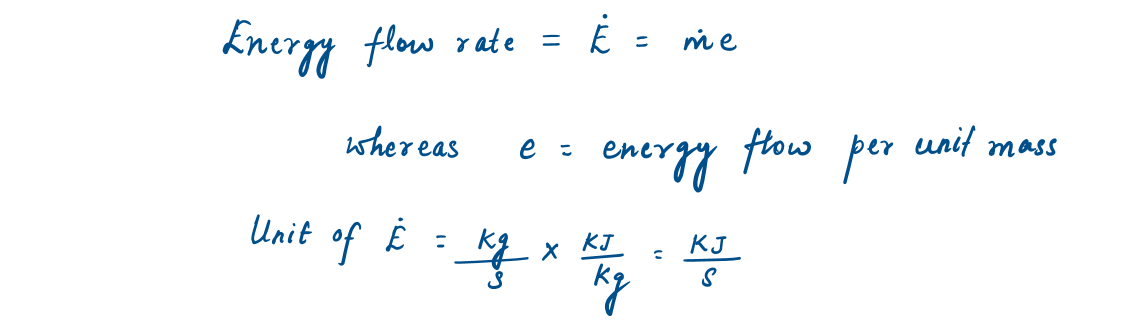
2.1.4 Mechanical Energy
The mechanical energy can be defined as the form of energy that can be converted to mechanical work completely and directly by an ideal mechanical device such as an ideal turbine.
Kinetic and potential energies are the familiar forms of mechanical energy.
Relation between mechanical and thermal energy
The frictional effects cause the mechanical energy to be lost (i.e., to be converted to thermal energy that usually cannot be used for any useful purpose). Thermal energy is not mechanical energy, however, since it cannot be converted to work directly and completely (the second law of thermodynamics). These systems do not involve the conversion of nuclear, chemical, or thermal energy to mechanical energy.
Difference between turbine and pump
A pump transfers mechanical energy to a fluid by raising its pressure, and a turbine extracts mechanical energy from a fluid by dropping its pressure. Therefore, the pressure of a flowing fluid is also associated with its mechanical energy.
Hence, the mechanical energy of a flowing fluid per unit mass will be
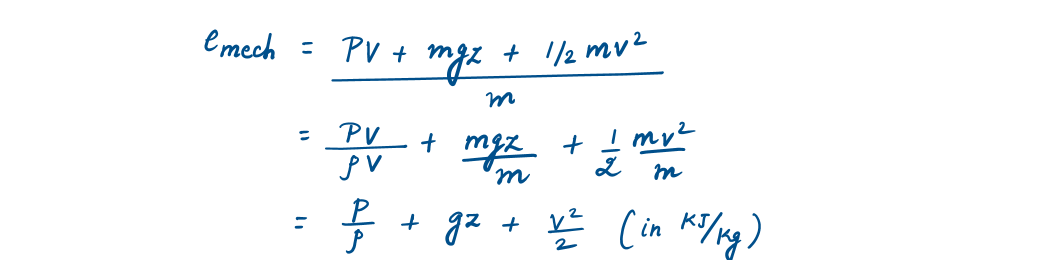
Similarly, Mechanical energy will be
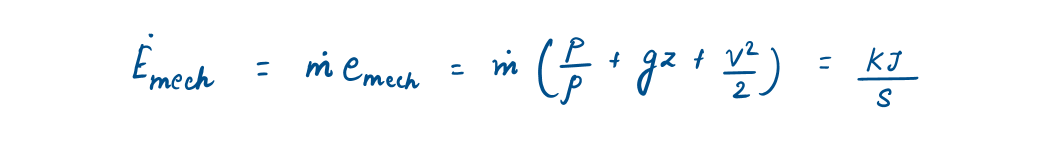
Then the mechanical energy change of a fluid during incompressible (p= constant) flow becomes
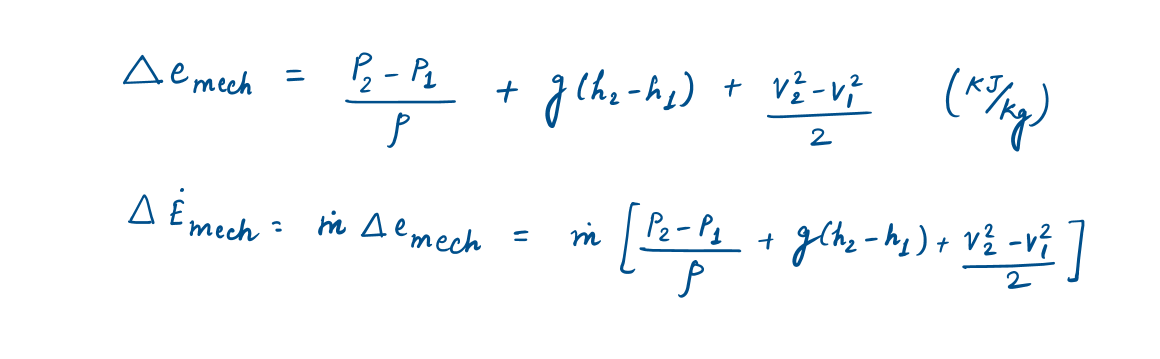
2.2 Energy Transfer by Heat
Energy can cross the boundary of a closed system in two distinct forms: heat and work.
Heat is defined as the form of energy that is transferred between two systems (or a system and its surroundings) by a temperature difference until thermal equilibrium is established (T surrounding = T system) and after this, energy transfer in the form of heat stops.


An energy interaction is heat only if it takes place because of a temperature difference. Heat is energy in transition. It is recognized only as it crosses the boundary of a system.
Adiabatic Process
A process during which there is no heat transfer is called an adiabatic process. There are two ways a process can be adiabatic:
-
The system is well insulated so that only a negligible amount of heat can pass through the boundary
- Both the system and the surroundings are at the same temperature and therefore there is no driving force (temperature difference) for heat transfer.
Mechanism for heat transfer
Heat is transferred by three mechanisms: conduction, convection, and radiation.
- Conduction- the transfer of energy from the more energetic particles of a substance to the adjacent less energetic ones as a result of interaction between particles.
- Convection- the transfer of energy between a solid surface and the adjacent fluid that is in motion, and it involves the combined effects of conduction and fluid motion.
- Radiation- the transfer of energy due to the emission of electromagnetic waves (or photons).
2.3 Energy Transfer by Work
Work is the energy transfer associated with a force acting through a distance. An energy interaction that is not caused by a temperature difference between a system and its surroundings is work.
Example- A rising piston, a rotating shaft, and an electric wire crossing the system boundaries are all associated with work interactions.
The work done per unit of time is called power (KJ/s or KW).
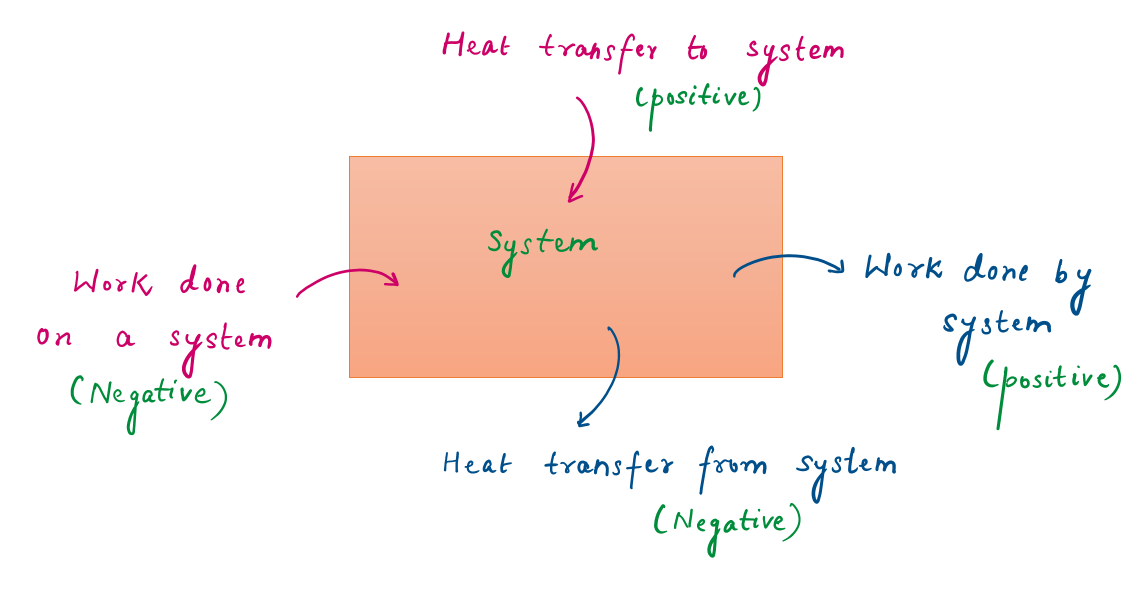
2.3.1 Sign Convection
- heat transfer to a system and work done by a system is positive;
- heat transfer from a system and work done on a system is negative
2.3.2 Similarities between Heat and Work
- Boundary Phenomena- Both are recognized at the boundaries of a system as they cross the boundaries.
- Systems possess energy, but not heat or work.
- Process- Both are associated with a process, not a state. Unlike properties, heat or work has no meaning in a state.
- Path Function- Both are path functions which means their magnitudes depend on the path followed during a process as well as the end states)
- Directional Quantities- Heat and work are directional quantities because the complete description of a heat or work interaction requires the specification of both the magnitude and direction.
The difference in calculation of Path function (Heat & work) and State function (Properties)
Path functions have inexact differentials designated by the symbol δ (partial derivative).
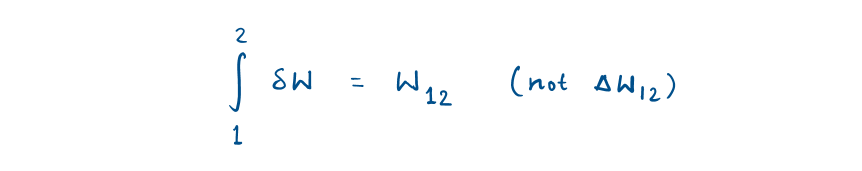
While properties (State or point function) have exact differential designated by d.
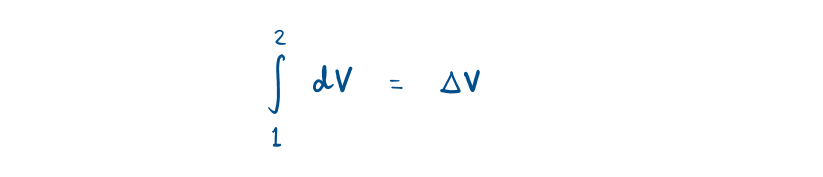
2.4 First Law of Thermodynamics
The first law of thermodynamics, also known as the conservation of energy principle states that energy can be neither created nor destroyed during a process; it can only change forms.
For all adiabatic processes between two specified states of a closed system, the total work done is the same regardless of the nature of the closed system and the details of the process. It means the value of the total work must depend on the end states of the system only, and thus it must correspond to a change in a property of the system. This property is total energy.
Example of Heat transfer without work interaction-
- a) The potato baked in the oven, then heat transfer to potato = Energy content of potato increases, neglecting mass transfer (moisture loss).

- b) The heating of water in a pan, Heat transfer to water - Heat lost to surrounding from water = Energy increase of water.

Example of work interaction without heat transfer-
- a) A well-insulated (i.e., adiabatic) room heated by an electric heater as our system: by conservation of energy, hence electrical work done on system = Increase in the energy of a system
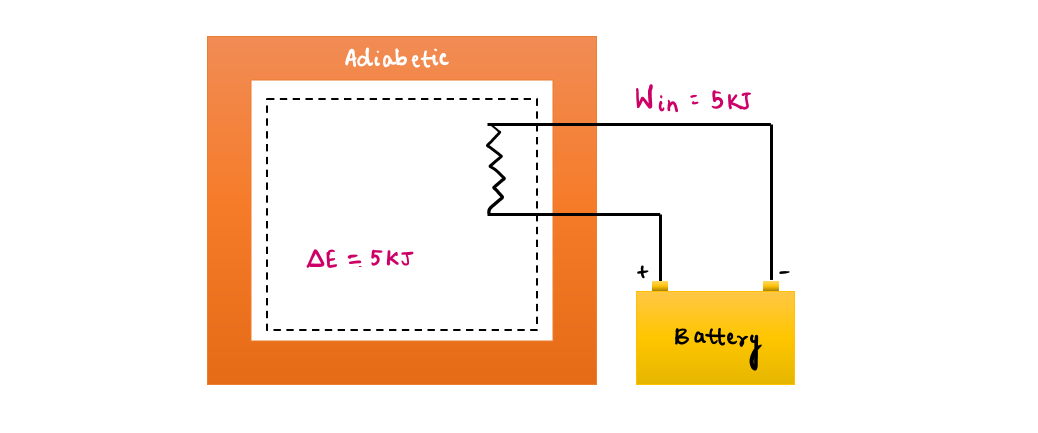
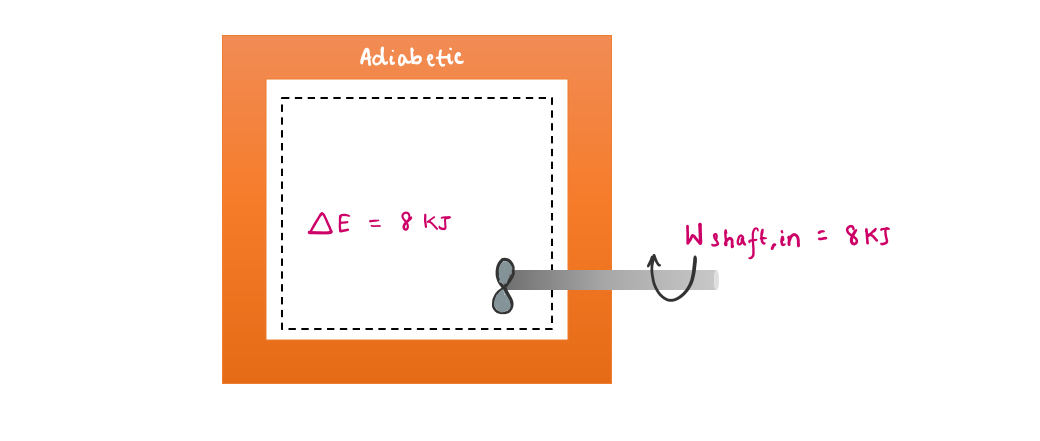
- b) From the above example, replace the electric heater with a paddle wheel. So as a result of the stirring process, shaft work done on the system = Increase in the energy of a system.
- c) The temperature of the air rises when it is compressed: This is because energy is transferred to the air in the form of boundary work. Hence, by the conservation of energy principle, an increase in the energy of the system = the boundary work done on the system.
2.4.1 Energy Balance
The net change (increase or decrease) in the total energy of the system during a process is equal to the difference between the total energy entering and the total energy leaving the system during that process.

This relation is often referred to as the energy balance and applies to any kind of system undergoing any kind of process.
2.4.2 Energy Change of a System
- The determination of the energy change of a system during a process involves the evaluation of the energy of the system at the beginning and the end of the process and taking their difference.
Energy change = Energy at final state - Energy at initial state
As energy is a property, so the value of a property does not change unless the state of the system changes.
- Energy can exist in numerous forms such as internal (sensible, latent, chemical, and nuclear), kinetic, potential, electric, and magnetic, and their sum constitutes the total energy E of a system. In the absence of electric, magnetic, and surface tension effects, the change in the total energy of a system during a process is the sum of the changes in its internal, kinetic, and potential energies
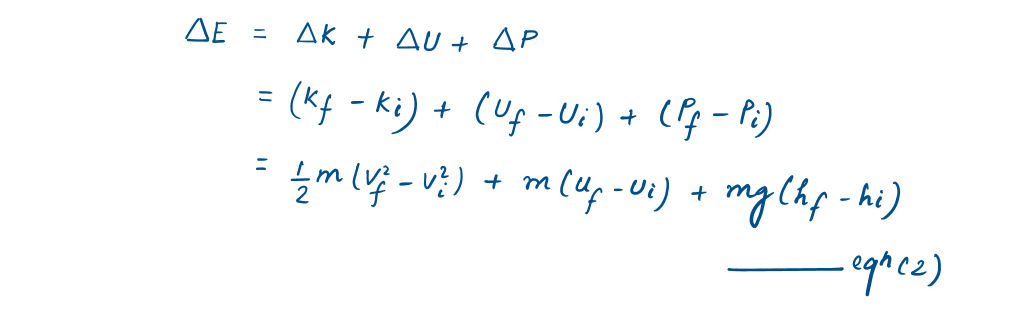
2.5 Mechanism of Energy Transfer
Energy can be transferred to or from a system in three forms: heat, work, and mass flow. Energy interactions are recognized at the system boundary as they cross it, and they represent the energy gained or lost by a system during a process.
The only two forms of energy interactions associated with a fixed mass or closed system are heat transfer and work.
Heat Transfer (Q)
Heat transfer to a system (heat gain) increases the energy of the molecules and thus the internal energy of the system and vice-versa.
Work Interaction (W)
An energy interaction that is not caused by a temperature difference between a system and its surroundings is work. Work transfer to a system increases the energy of the system or vice-versa.
Car engines and hydraulic, steam, or gas turbines produce work while compressors, pumps, and mixers consume work.
A rising piston, a rotating shaft, and an electrical wire crossing the system boundaries are all associated with work interactions.
Mass Flow (m)
Mass flow in and out of the system serves as an additional mechanism of energy transfer. When mass enters a system, the energy of the system increases because mass carries energy with it or vice-versa.
For example, when some hot water is taken out of a water heater and replaced by the same amount of cold water, the energy content of the hot-water tank (the control volume) decreases due to this mass interaction.
Then, the energy balance can be written more explicitly as (from equation [1])
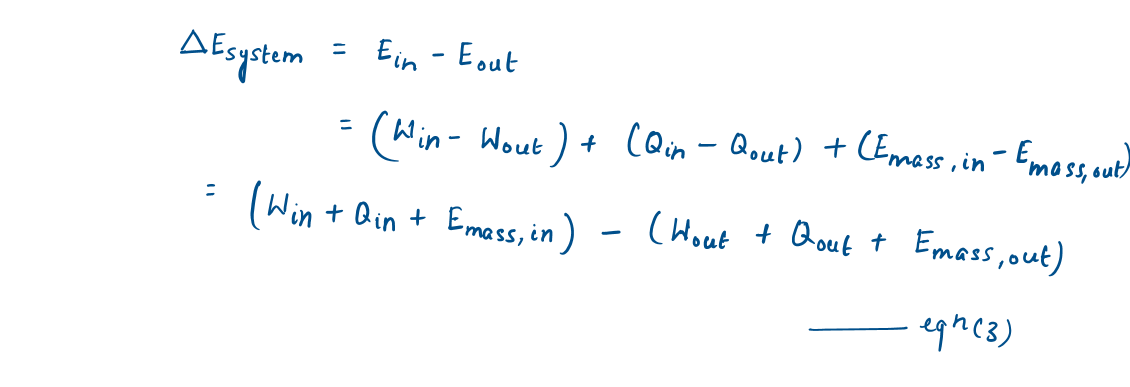
Representation of Energy balance equation in different forms
In rate form (per unit time),
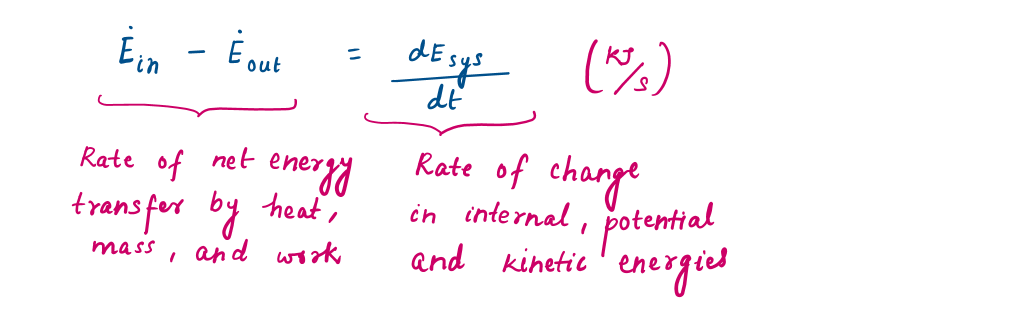
For mass per unit,

2.6 Efficiencies of Mechanical and Electrical Devices
Mechanical efficiency-
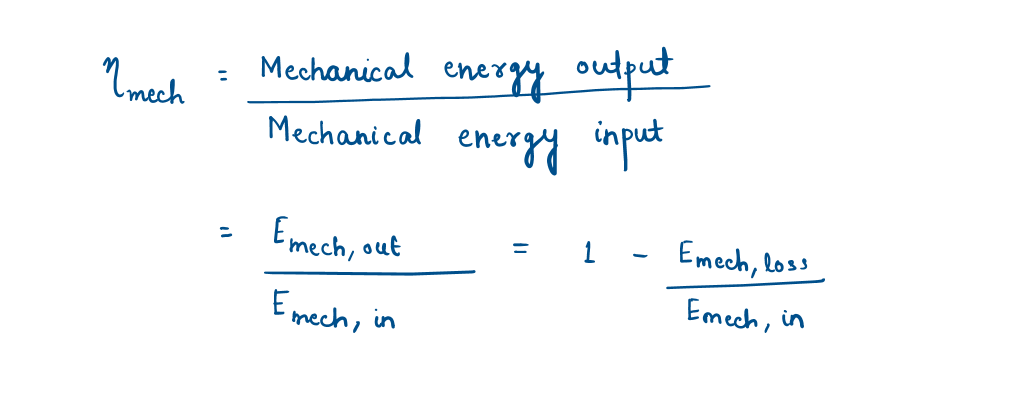
Pump and Pump Efficiency
A pump or a fan receives shaft work (usually from an electric motor) and transfers it to the fluid as mechanical energy (less frictional losses) to increase of pressure, velocity, and elevation of fluid.
The degree of perfection of the conversion process between the mechanical work supplied and the mechanical energy of the fluid is expressed by the pump efficiency-
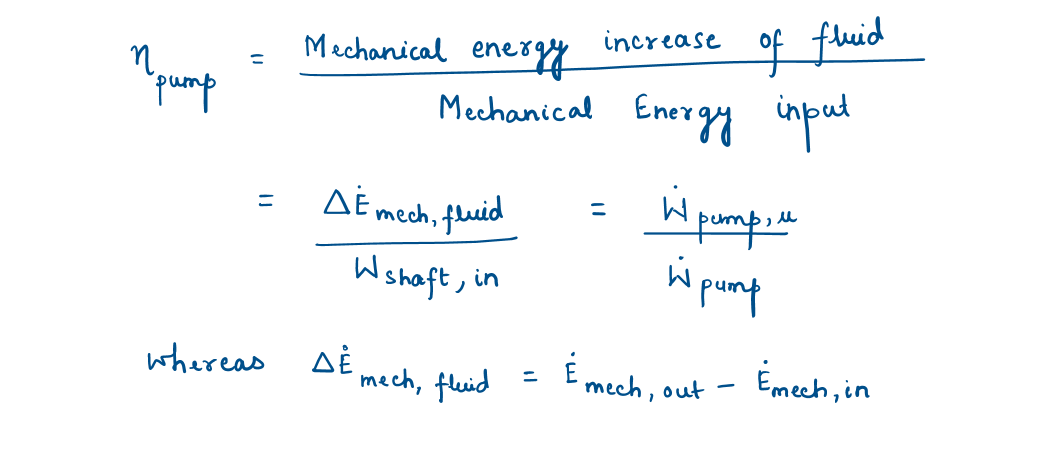
Turbine and Turbine Efficiency
A turbine converts the mechanical energy of a fluid to shaft work. Turbines extract mechanical energy from a fluid and produce mechanical power in the form of a rotating shaft that can drive a generator or any other rotary device.
Turbine efficiency can be defined as:
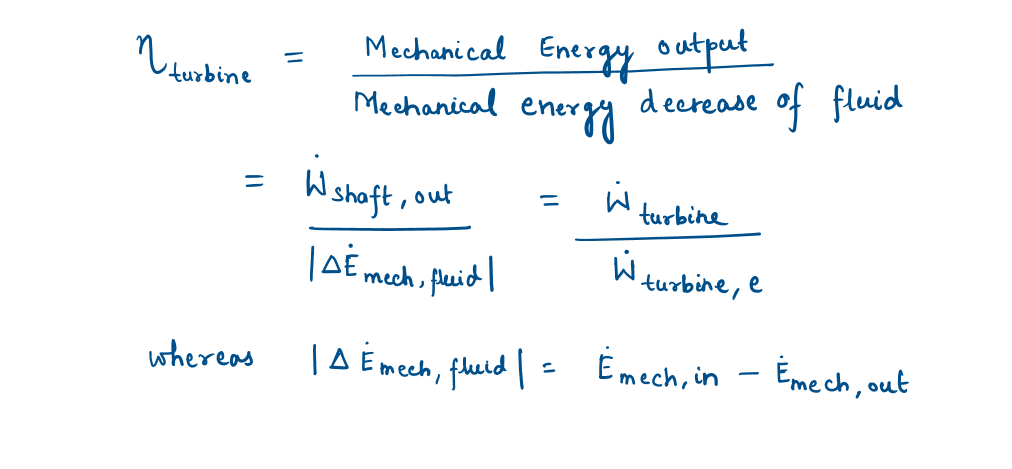
A pump or turbine efficiency of 100 percent indicates perfect conversion between the shaft work and the mechanical energy of the fluid, and this value can be approached (but never attained) as the frictional effects are minimized.
Motor
Electrical energy is converted to rotating mechanical energy by electric motors to drive fans, compressors, robot arms, and car starters.

Generator
A generator is a device that converts mechanical energy to electrical energy.
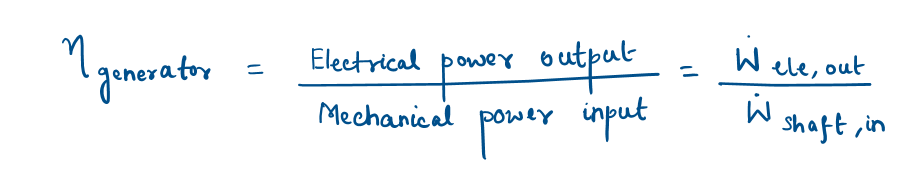
Overall efficiency of pump–motor
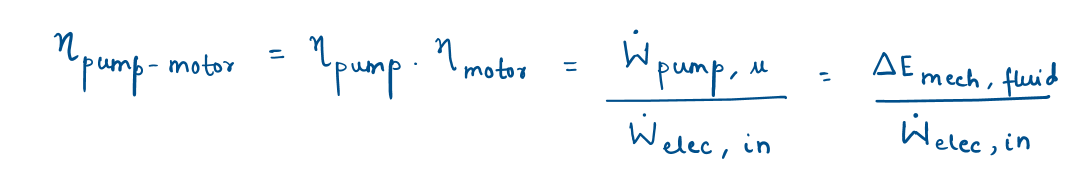
Overall efficiency of turbine-generator
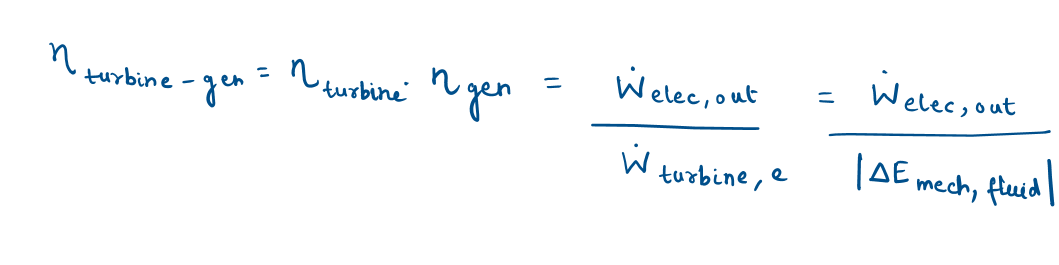

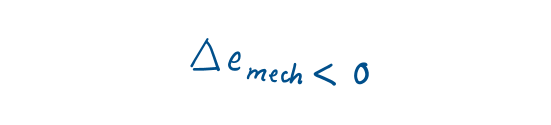
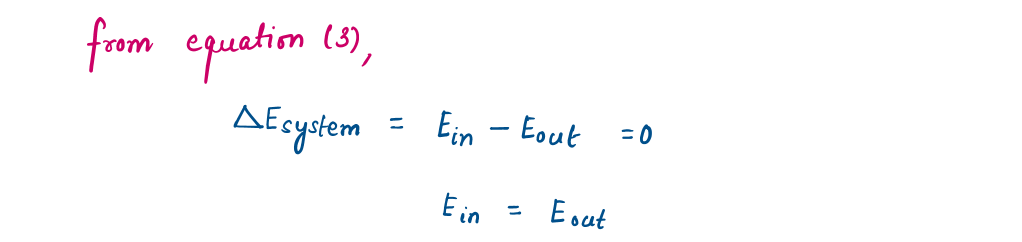
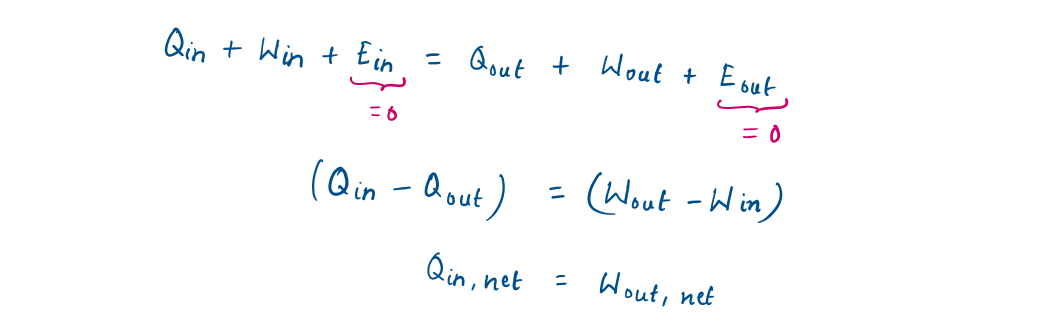
Unit 2: Energy Transfer and General Energy Analysis